Common Core Math Commutative Property

Commutative Holding

The commutative property states that the numbers on which nosotros operate tin be moved or swapped from their position without making any divergence to the reply. The property holds for Addition and Multiplication, merely non for subtraction and partition. Allow's see.

Commutative property for addition, Subtraction, multiplication and division

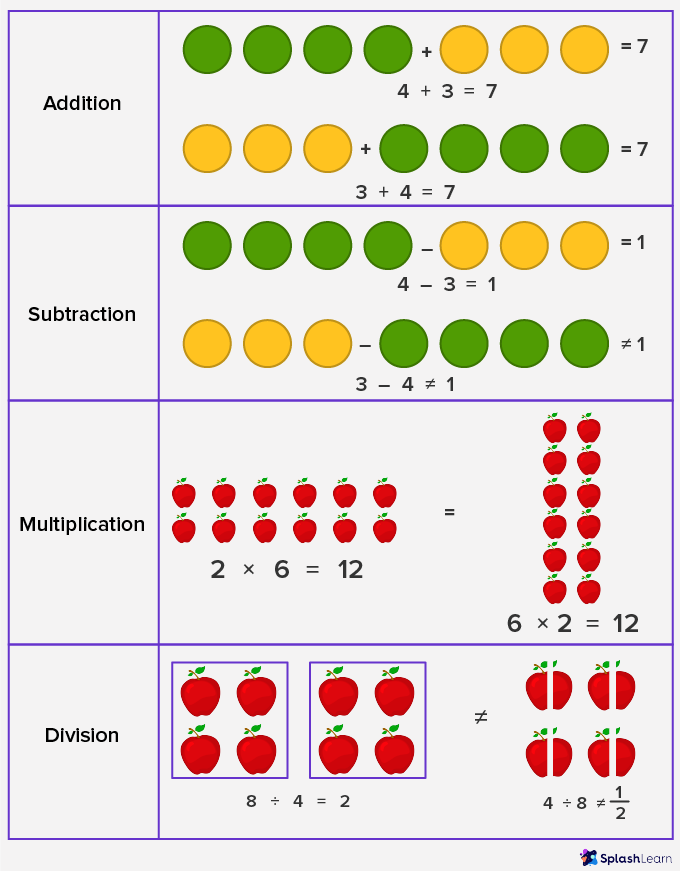
The above examples clearly testify that the commutative property holds true for addition and multiplication simply not for subtraction and division. So, if we swap the position of numbers in subtraction or partition statements, it changes the unabridged problem.

So, mathematically commutative property for addition and multiplication looks like this:

Commutative Holding of Improver:

a + b = b + a; where a and b are any 2 whole numbers

Commutative Property of Multiplication:

a × b = b × a; where a and b are any 2 nonzero whole numbers

Employ Cases of Commutative Belongings

Myra has 6 apples and two peaches. Kim has ii apples and half dozen peaches. Who has more than fruits?

Even if both have different numbers of apples and peaches, they have an equal number of fruits, because 2 + 6 = 6 + 2.

Sara buys three packs of buns. Each pack has four buns. Mila buys 4 packs of buns and each pack has 3 buns. Who bought more buns?

Even if both have different numbers of bun packs with each having a dissimilar number of buns in them, they both bought an equal number of buns, considering 3 × iv = 4 × 3.

Solved Examples on Commutative Property

Example 1: Fill in the missing numbers using the commutative property.

_________ + 27 = 27 + 11
45 + 89 = 89 + _________
84 × ______ = 77 × 84
118 × 36 = ________ × 118

Solution:

eleven; by commutative property of add-on
45; by commutative property of add-on
77; by commutative property of multiplication
36; by commutative property of multiplication

Example 2: Utilise fourteen × 15 = 210, to notice 15 × 14.

Solution:

Equally per commutative property of multiplication, 15 × 14 = 14 × 15.

Since, 14 × 15 = 210, so, 15 × 14 also equals 210.

Example three: Utilise 827 + 389 = i,216 to find 389 + 827.

Solution:

As per commutative property of addition, 827 + 389 = 389 + 827.

Since, 827 + 389 = i,216, so, 389 + 827 too equals ane,216.

Example 4: Utilize the commutative property of improver to write the equation, 3 + five + 9 = 17, in a different sequence of the addends.

Solution:

iii + 9 + five = 17 (because 5 + 9 = nine + 5)

5 + iii + 9 = 17 (because 3 + 5 = 5 + 3)

v + 9 + 3 = 17 (because 3 + 9 = 9 + 3)

Similarly, nosotros can rearrange the addends and write:

9 + iii + 5 = 17

9 + 5 + 3 = 17

Example iv: Ben bought three packets of six pens each. Mia bought vi packets of 3 pens each. Did they buy an equal number of pens or non?

Solution:

Ben bought three packets of 6 pens each.

And then, the total number of pens that Ben bought = 3 × half dozen

Mia bought 6 packets of 3 pens each.

So, the total number of pens that Ben bought = 6 × iii

By the commutative property of multiplication, 3 × 6 = 6 × three.

So, both Ben and Mia bought an equal number of pens.

Example v: Lisa has 78 cerise and 6 bluish marbles. Beth has 6 packets of 78 marbles each. Do they accept an equal number of marbles?

Solution:

Since Lisa has 78 blood-red and 6 blue marbles.

Then, the total number of marbles with Lisa = 78 + 6

Beth has 6 packets of 78 marbles each.

So, the full number of marbles with Beth = half-dozen × 78

Conspicuously, calculation and multiplying ii numbers gives dissimilar results. (Except 2 + ii and two × 2.

That is, 78 + 6 ≠ half-dozen × 78

Then, Lisa and Beth don't accept an equal number of marbles.

Practice Problems

Commutative Holding

Attend this Quiz & Test your knowledge.

8 + 5 = 5 + 8

8 × 5 = five × 8

viii + v = viii – 5

viii + 5 = 5 × eight

Correct reply is: 8 + five = 5 + 8
According to the commutative property of addition, the sum remains the same on interchanging the addends. That is, a + b = b + a.

7 × $\frac{one}{seven}$ = one

7 × 1 = 7

7 × three = 3 × seven

vii × 0 = 0

Right answer is: 7 × 3 = iii × 7
According to the commutative belongings of multiplication, the product remains the same on interchanging the multiplicand and multiplier. That is, a × b = b × a.

15 ÷ 3

15 × three

15 – 3

3 ÷ fifteen

Correct answer is: fifteen × 3
Commutative property does not agree true for division and subtraction.

five, five

4, iv

five, 4

4, v

Correct answer is: four, v
five + iv = 4 + 5
(by commutative property of addition)

Often Asked Questions

Can you apply the commutative property of add-on/multiplication to 3 numbers?

Yes. By definition, commutative belongings is applied on 2 numbers, but the result remains the same for 3 numbers as well. This is considering we can use this property on two numbers out of three in various combinations.

Which operations do not follow commutative belongings?

Commutative holding cannot be practical to subtraction and division.

What is the associative property of addition (or multiplication)?

This property states that when three or more than numbers are added (or multiplied), the sum (or the production) is the same regardless of the grouping of the addends (or the multiplicands). That is,

(a + b) + c = a + (b + c)
(a × b) × c = a × (b × c) where a, b, and c are whole numbers.

For which all operations does the associative property concord true?

The Associative belongings holds truthful for improver and multiplication.

What is the distributive property of multiplication?

Past the distributive property of multiplication over addition, we hateful that multiplying the sum of two or more addends by a number will give the same outcome every bit multiplying each addend individually by the number and then adding the products together. That is,

a × (b + c) = (a × b) + (a × c) where a, b, and c are whole numbers.